好幾個粉絲留言讓W君聊聊美國最新的量子計算芯片Willow,這有點太看得起W君了。
我們就是一個做軍事情報分析的分析狗,聊這個東西似乎就有點跨界了。
但是,W君還是可以從按照軍事情報分析的框架來給大家聊聊,爲了避免下作的蹭流量,咱們就把Willow直接翻譯成它的意譯“小魔仙”,同時,咱們也不去提這個“小魔仙”的創造公司的名字,畢竟這個名字也是個流量熱詞。
首先,從本質上來說小魔仙芯片的確是實現了一個質的突破,讓人們看到量子計算機實用化的可能性,這是小魔仙芯片的消息發布後最有價值的部分。
簡單的說一下“爲什么”。任何計算機的理論都是在一個相對於理想的狀態下實現的。但是從工程學上來說理想狀態是不可能實現的。例如在我們的計算機上存儲一個最小的數據單位——比特,這實際上就是存儲單元中的高低電平的變化。一般的來說,高電平爲1、低電平爲0。
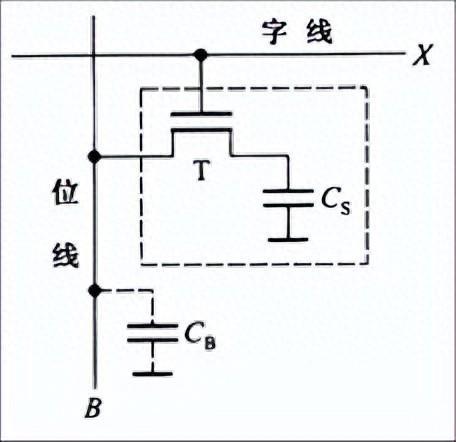
從電路圖上我們就可以看到,傳統計算機的存儲單元一般是由電容或者mos或者三極管來組成。在其中存儲的電荷的多少代表了高低電平,當然了,還有磁性元件或者光存儲元件。這些存儲單元的特點都在於狀態可以翻轉來代表0或者1。
只不過,大部分存儲狀態都會被環境的影響所改變。即便是光盤這種看似穩定的存儲介質也可能因爲物理上的劃痕造成內部所存儲的數據失真。

更別提傳統的計算機內存了。只不過,在傳統的計算機中我們一般並不會因爲這些環境影響所帶來的計算機數據“失真”而帶來計算上的錯誤。究其原因在於我們的計算機本身是帶有“糾錯”的功能的。舉個例子——當我們存儲一個信息的時候入如果一個比特位上的數據是1,但是有可能因爲電磁的影響把這個1變成了0,這樣我們存儲的信息就沒有置信度了,通過沒有置信度的數據所計算出的結果也就可能是錯誤的了,這樣計算機就失去了實用價值。怎么辦我們可以在三個比特的範圍內存儲一個比特的數據,例如我們在三個比特的位置上存儲111,當有環境影響的時候改變了一個比特位,那么我們可以通過“少數服從多數”的原則依舊得到准確的數據,例如111、011、101、110都會被當作“1”來看待。

其實光盤存儲介質上存儲數據的方法就是借助於這樣的准則來建立的,傳統文檔中我們說在激光頭在光盤上留下小坑或者小點,但很少有人告訴你這個小點是長條狀的。在光盤讀取的時候正因爲是長條狀的點的存在,所以細小的劃痕才不會有影響——但要注意的是我們犧牲掉了2/3的存儲密度,這就是一個取舍了。
在計算機傳輸過程中,我們還有奇偶校驗碼者漢明碼來支持各種不同方向上的數據糾錯。也正因爲這些糾錯有效工作我們的計算機才可以實用化。
現在說回“小魔仙”芯片,在發布會上最重要的一張圖是下面這張:

這個東西是什么?這是“表面碼”(Surface code)。是一種更高效的糾錯方式,還是以“少數服從多數”的糾錯方式來說,一個量子位上不僅僅會存儲0和1的疊加態,還會存儲量子位的波動態我們可以理解爲-和+,因此一個量子位的存儲會是 -0,+0,-1,+1,這樣我們要存儲糾錯狀態的時候就需要先存儲數據的糾錯 還是三個1,也就是111,然後再用少數服從多數的方式存儲 +111、+111、+111,這樣就形成了下面九個量子位的存儲方式
+111
也就是說利用九個量子位才可以確保數據的穩定性。這種方式在實際上是效率極低的,而且對於這種方式的校驗所付出的成本遠大於這種方式帶來的計算收益。
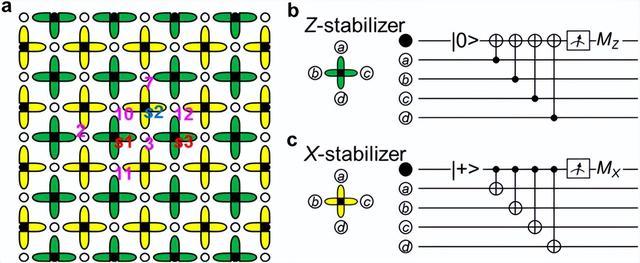
在計算機拓撲學中有一個糾錯方式叫做表面碼,它是利用紀錄拓撲形態進行糾錯的,所以你看小魔仙芯片的發布會中最重要的那張圖,其實就是把表面碼的原理圖旋轉了45度。它才真正的揭示了小魔仙芯片的核心價值。

簡單說概念,大家拿起自己的手機仔細看屏幕中的像素點,手機屏幕的像素點越多顯示的圖像就越細致。表面碼也是如此,當“表面點”越多就越能顯示(表現)更細致的拓撲結構。因此在表面碼的加持下理論上量子比特位越多,糾錯的能力就越強。而且由於是拓撲計算,因此在達到了一定的“像素”密度下驗證正確與否的开銷就會趨近於下降的趨勢。例如我們做個試驗,下面的圖形的大小都是一樣的。




第一張圖的像素是10個像素的,因此你只可以看到藍綠灰色的色塊,第二張圖是100像素,你可以看到海邊的椰子樹,到了第三張圖500像素的時候你可以看清海邊椰子樹下有一張躺椅,到了第四張圖1000像素的時候你卻不會從圖像中再發現更多細節了。其實到500像素的時候你的“拓撲識別”就固定到了一個开銷平衡的水准。這就是大家能理解的表面碼算法。你的眼睛看所有圖形的時間也只是0.1秒就能識別到圖形上的大部分信息——开銷趨近於平衡。
小魔仙芯片的最大驗證價值就是驗證了在量子計算領域內,我們可以利用表面碼技術完成量子計算的糾錯,並且在一定數量的量子數量下實現了驗證數據准確性(糾錯)比計算任務本身的的开銷更低的可能性,也就是說,從這一刻起真正可能不存在錯誤的量子計算成爲一種可能。

除此之外,小魔仙的芯片並不代表什么。
那爲什么說美國給中國創造了一個神話呢?其實是說咱們的自媒體,盲目蹭流量的問題了。

問題來源於這個數據在隨機電路採樣測試中,小魔仙芯片用了5分鐘的時間完成了地球上現有的超級計算機10000000000000000000000000年的計算量。
這件事我們看發布會的PPT原圖,小魔仙5分鐘,經典超級計算機10000000000000000000000000年。這就被自媒體拿來炒作了。
但是,說這個計算能力炸裂的前提是先要了解一下什么是隨機電路取樣(random Circuit Sampling,RCS), 是一種量子計算的基准算法,用於驗證量子計算機是否能完成經典計算機無法處理的復雜任務。它通過在一組量子比特上運行隨機生成的量子邏輯門,讓比特進入高度糾纏和疊加的狀態,然後測量輸出結果,生成一個復雜的概率分布。經典計算機在模擬這種分布時需要記錄所有可能的量子態,其數量隨着比特數量呈指數級增長(例如 53 個比特需記錄 2⁵³ 個狀態)。此外,隨機電路的深度增加會顯著提升計算復雜度,使經典算法無法找到有效的近似方法。這使得 RCS 成爲驗證“量子優越性”的重要工具,也是量子計算機展示潛力的核心實驗之一。
只不過要注意的一點是,RCS僅是驗證量子優越性的重要工具而已,並不具備真正的實際應用價值。說個大家都理解的概念——如果一台計算機被設計成3D Mark的專用跑分機器,而不能玩任何遊戲,那么這台計算機就除了跑分之外沒有了任何意義。

小魔仙芯片目前就是這種計算機、而RCS就等同於我們現實生活中的3D Mark。
很多自媒體的認知就把這種跑分機當作通用計算機了,腦洞大开,認爲“小魔仙芯片”成了改變人類進程的驚世之作……硬生生的造神話,不尷尬嗎?

所謂宇宙級的轟動、芯片的革命、證明平行宇宙、加密貨幣終結者……都是初中沒上完的自媒體作者們的臆斷。
本質上,“專用機”是沒有任何實際意義的。
不信嗎?那W君給大家構建一個專用計算機系統:
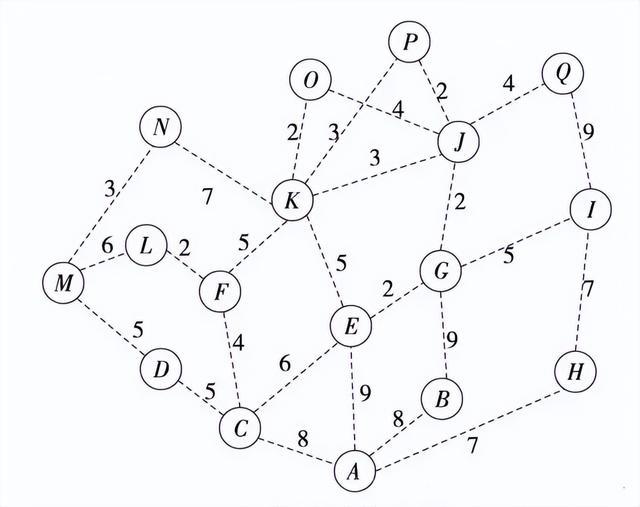
在數學領域“圖論”中有一個很經典的難題,叫做兩點之間最小距離。類似於上面的圖要求迅速的求出圖中任意兩點之間的最近距離。圖由節點和節點之間的距離來構成,例如上圖A和B的距離爲8,A和E點距離是9……那么我們如何求出J到L點的最短距離和路徑呢 是JKFL還是JQIGBZCFL或者是其他?
經典計算機的方式就是遍歷所有節點的可能性,然後經過排序找出這些可能性中最小的一個。隨着節點數量的增加,其實這個圖計算的復雜度也和RCS的復雜度一樣是以指數級上升的。
那么W君要用什么方式構建一個專用“計算機”來解決復雜到傳統計算機要幾萬年到幾億年的計算呢?答案是只需要一些繩子,一根釘子和一個熱氣球。
1.在輸入圖結構的時候,按照圖來剪出合適長度的繩子,例如M-L就剪出6米長的繩子,N-M就剪出3米長的繩子
2.將繩子按照節點的次序系在一起形成圖
這個計算機就構建完成了
在計算的時候只需要在想計算的起始節點的繩結上拴上一個氣球,把目的節點的繩結釘在地面上。
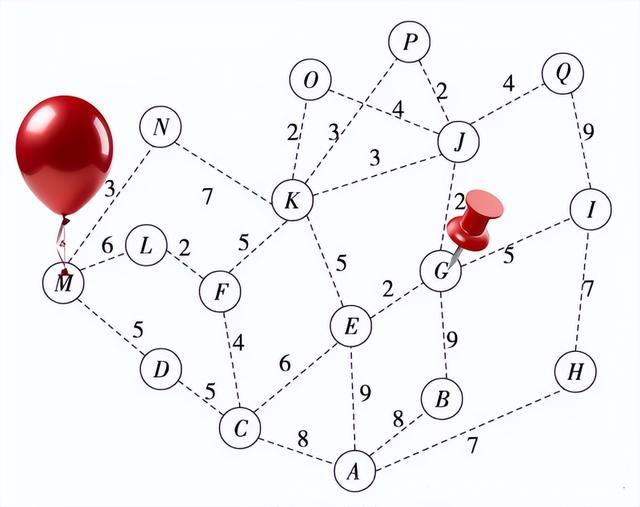
松开手就能得到計算結果。——這只網會在氣球的浮力作用下直接被拉伸,最終停留在最短的路徑上,理論上,如果節點的數量達到一定的量級後,只要氣球的浮力足夠大,那么“繩子計算”可以完虐“經典的超級計算機”。
那么是不是W君就創造了一個繩子計算機也得被很多自媒體博主大吹特吹呢?但問題是,這種繩子計算機除了解決無矢量圖最短路徑問題之外其實也是毫無價值的。
按照現在的自媒體博主們的邏輯就應該大吹特吹了,題目都可以幫他們想好了《中國低功耗計算機开物理掛,秒殺美國計算機10萬萬萬萬億年》。
講真,美國這個芯片其實挺好,但真沒好到現在大家說的這個地步,而且只是驗證了糾錯所帶來的附加計算的开銷在可接受的程度範圍內。如果指望着這種芯片可以真正的有那怕一點用途目前來說還是太過於遙遠了。被1萬萬萬億年的一頁PPT忽悠傻了吧?這其實就是碎片化信息傳播帶來的致命問題了,哪怕一個詞露出來到我們這裏怎么就成了神話了?在高呼美國萬萬萬億年的時候,拜托你知道RCS到底是個啥嗎?
特別聲明:以上文章內容僅代表作者本人觀點,不代表新浪網觀點或立場。如有關於作品內容、版權或其它問題請於作品發表後的30日內與新浪網聯系。標題:說說美國的量子計算芯片Willow,美國給中國創造了神話
地址:https://www.utechfun.com/post/454907.html
